Contents |
Frequency of 5 card poker hands
The following enumerates the frequency of each hand, given all combinations of 5 cards randomly drawn from a full deck of 52, without wild cards. The probability is calculated based on 2,598,960, the total number of 5 card combinations. Here, the probability is the frequency of the hand divided by the total number of 5 card hands, and the odds are defined by (1/p) − 1 : 1, where p is the probability. (The frequencies given are exact; the probabilities and odds are approximate.)
| Hand | Frequency | Probability | Odds against |
|---|---|---|---|
| Royal flush | 4 | 0.00000154 % | 649,740 : 1 |
| Straight flush | 36 | 0.0000154 % | 64,973 : 1 |
| Four of a kind | 624 | 0.0240 % | 4,164 : 1 |
| Full house | 3,744 | 0.144 % | 693 : 1 |
| Flush | 5,108 | 0.197 % | 508 : 1 |
| Straight | 10,200 | 0.392 % | 254 : 1 |
| Three of a kind | 54,912 | 2.11 % | 46.3 : 1 |
| Two pair | 123,552 | 4.75 % | 20.0 : 1 |
| One pair | 1,098,240 | 42.3 % | 1.37 : 1 |
| No pair | 1,302,540 | 50.1 % | 0.995 : 1 |
| Total | 2,598,960 | 100 % | 1 : 1 |
The royal flush is also included as a straight flush above. The royal flush can be formed 4 ways (one for each suit), giving it a probability of 0.000001539077169 and odds of 649,740 : 1.
When ace-low straights and straight flushes are not counted, the probabilities of each are reduced: straights and straight flushes become 9/10 as common as they otherwise would be.
Derivation
The following computations show how the above frequencies were determined. To understand these derivations, the reader should be familiar with the basic properties of the binomial coefficients and their interpretation as the number of ways of choosing elements from a given set. See also: sample space and event (probability theory).
- Straight flush — Each straight flush is uniquely determined by its highest ranking card; and these ranks go from 5 (A-2-3-4-5) up to A (T-J-Q-K-A) in each of the 4 suits. Thus, the total number of straight flushes is:
- Four of a kind — Any one of the thirteen ranks can form the four of a kind, leaving 52 − 4 = 48 possibilities for the final card. Thus, the total number of four-of-a-kinds is:
- Full house — The full house comprises a triple (three of a kind) and a pair. The triple can be any one of the thirteen ranks, and three of the four cards of this rank are chosen. The pair can be any one of the remaining twelve ranks, and two of the four cards of the rank are chosen. Thus, the total number of full houses is:
- Flush — The flush contains any five of the thirteen ranks, all of which belong to one of the four suits, minus the 40 straight flushes. Thus, the total number of flushes is:
- Straight — The straight consists of any one of the ten possible sequences of five consecutive cards, from 5-4-3-2-A to A-K-Q-J-T. Each of these five cards can have any one of the four suits. Finally, as with the flush, the 40 straight flushes must be excluded, giving:
- Three of a kind — Any of the thirteen ranks can form the three of a kind, which can contain any three of the four suits. The other cards can have any two of the remaining twelve ranks, and each can have any one of the four suits. Thus, the total number of three-of-a-kinds is:
- Two pair — The pairs can have any two of the thirteen ranks, and each pair can have two of the four suits. The final card can have any one of the eleven remaining ranks, and any suit. Thus, the total number of two-pairs is:
- Pair — The pair can have any one of the thirteen ranks, and any two of the four suits. The remaining three cards can have any three of the remaining twelve ranks, and each can have any of the four suits. Thus, the total number of pair hands is:
- No pair — A no-pair hand contains five of the thirteen ranks, discounting the ten possible straights, and each card can have any of the four suits, discounting the four possible flushes. Alternatively, a no-pair hand is any hand that does not fall into one of the above categories; that is, any way to choose five out of 52 cards, discounting all of the above hands. Thus, the total number of no-pair hands is:
Frequency of 7 card poker hands
In some popular variations of poker, a player uses the best five-card poker hand out of seven cards. The frequencies are calculated in a manner similar to that shown for 5-card hands, except additional complications arise due to the extra two cards in the 7 card poker hand.[1] The total number of distinct 7-card hands is 133,784,560. It is notable that the probability of a no-pair hand is less than the probability of a one-pair or two-pair hand. (The frequencies given are exact; the probabilities and odds are approximate.)
| Hand | Frequency | Probability | Odds against |
|---|---|---|---|
| Straight flush | 41,584 | 0.03108 % | 3,216 : 1 |
| Four of a kind | 224,848 | 0.1681 % | 594 : 1 |
| Full house | 3,473,184 | 2.60 % | 37.5 : 1 |
| Flush | 4,047,644 | 3.03 % | 32.1 : 1 |
| Straight | 6,180,020 | 4.62 % | 20.6 : 1 |
| Three of a kind | 6,461,620 | 4.83 % | 19.7 : 1 |
| Two pair | 31,433,400 | 23.5 % | 3.26 : 1 |
| One pair | 58,627,800 | 43.8 % | 1.28 : 1 |
| No pair | 23,294,460 | 17.4 % | 4.74 : 1 |
| Total | 133,784,560 | 100 % | 0 : 1 |
See also
Poker topics:
Math and probability topics:
External links
- MathWorld: Poker
- Probability and Poker
- Brian Alspach's mathematics and poker page
- Poker probabilities including conditional calculations
- Numerous poker probability tables
- 5, 6, and 7 card poker probabilities
- Preflop, After Flop and Chance of Making Hand Odds
-
Poker Game at Net Casino
Categories: Poker gameplay and terminology




 216.73.216.104
216.73.216.104 User Stats:
User Stats:
 Today: 0
Today: 0 Yesterday: 0
Yesterday: 0 This Month: 0
This Month: 0 This Year: 0
This Year: 0 Total Users: 117
Total Users: 117 New Members:
New Members:
 216.73.xxx.xxx
216.73.xxx.xxx
 Server Time:
Server Time: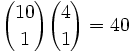
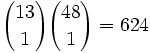
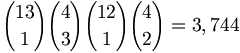
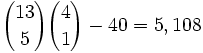
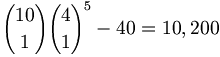
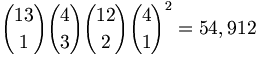

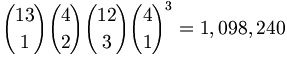
 = {52 \choose 5} - 1,296,420 = 1,302,540](./modules/Gambling_Guide/images/30fe9f0dc3c05be75318bd9afe703308.png)
