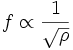Music Sound

In music, pitch is the psychological correlate of the fundamental frequency of a note.

Contents 1 Perception of pitch 2 Examples 3 Concert pitch 4 Labeling pitches 5 Varying pitch 6 Scales 7 Other musical meanings of pitch 8 Historical pitch standards 9 Need to standardize pitch 10 Changing the pitch of a vibrating string 10.1 Length 10.2 Tension 10.3 Density 11 Sources 12 External links

Perception of pitch

Like other senses, the relative perception of pitch can be fooled, resulting in "audio illusions". There are several of these, such as the tritone paradox, but most notably the Shepard scale, where a continuous or discrete sequence of specially formed tones can be made to sound like this sequence continues ascending forever, when this in fact is an audio illusion.

Examples

The note A above middle C played on any instrument is perceived to be of the same pitch as a pure tone of 440 Hz, but does not necessarily contain a partial having that frequency. Furthermore, a slight change in frequency need not lead to a perceived change in pitch, but a change in pitch implies a change in frequency. In fact, the just noticeable difference (the threshold at which a change in pitch is perceived) is about five cents, but varies over the range of hearing and is more precise when the two pitches are played simultaneously. Like other human stimuli, the perception of pitch also can be explained by the Weber-Fechner law. Pitch also depends on the amplitude of the sound, especially at low frequencies. For instance, a low bass note will sound lower in pitch if it is louder. Like other senses, the relative perception of pitch can be fooled, resulting in "audio illusions". There are several of these, such as the tritone paradox, but most notably the Shepard scale, where a continuous or discrete sequence of specially formed tones can be made to sound like this sequence continues ascending forever, when this in fact is an audio

Concert pitch

The A above middle C is nowadays set at 440 Hz (often written as "A = 440 Hz" or sometimes "A440", and known as concert pitch), although this has not always been the case (see "Historical pitch standards"). Pitch is often cited as one of the fundamental aspects of music.

Labeling pitches

Pitches are often labeled using scientific pitch notation or some combination of a letter and a number representing a fundamental frequency. For example, one might refer to the A above middle C as "A4" or "A440." However, there are two problems with this practice. First, in standard Western equal-temperament, the notion of pitch is insensitive to spelling: the description "G##4" refers to the same pitch as "A4." Second, human pitch perception is logarithmic with respect to fundamental frequency: the perceived distance between the pitches "A220" and "A440" is the same as the perceived distance between the pitches "A440" and "A880."

To avoid these problems, music theorists sometimes represent pitches using a numerical scale based on the logarithm of fundamental frequency. For example, one can adopt the widely-used MIDI standard to map fundamental frequency f to a real number p as follows

p = 69 + 12 * log₂(f / 440)

This creates a linear pitch space in which octaves have size 12, semitones (the distance between adjacent keys on the piano keyboard) have size 1, and middle C is assigned the number 60. Distance in this space corresponds to musical distance as measured in psychological experiements and understood by musicians. The system is flexible enough to include "microtones" not found on standard piano keyboards. For example, the pitch halfway between C (60) and C# (61) can be labeled 60.5.

Varying pitch

Pitches may be described in various ways, including high or low, as discrete or indiscrete, pitch that changes with time (chirping) and the manner in which this change with time occurs: gliding; portamento; or vibrato, and as determinate or indeterminate. Musically the frequency of specific pitches is not as important as their relationships to other frequencies - the difference between two pitches can be expressed by a ratio or measured in cents. People with a sense of these relationships are said to have relative pitch while people who have a sense of the actual frequencies independent of other pitches are said to have absolute pitch, less accurately called perfect pitch.

Scales

The relative pitches of individual notes in a scale may be determined by one of a number of tuning systems. In the west, the twelve-note chromatic scale is the most common method of organization, with equal temperament now the most widely used method of tuning that scale. In it, the pitch ratio between any two successive notes of the scale is exactly the twelfth root of two (or about 1.05946). In well-tempered systems (as used in the time of Johann Sebastian Bach, for example), different methods of musical tuning were used. Almost all of these systems have one interval in common, the octave, where the pitch of one note is double the frequency of another. For example, if the A above middle C is 440 Hz, the A an octave above that will be 880 Hz.

Other musical meanings of pitch

In atonal, twelve tone, or musical set theory a "pitch" is a specific frequency while a pitch class is all the octaves of a frequency. Pitches are named with integers because of octave and enharmonic equivalency (for example, C# and Db are the same pitch while C4 and C5 are functionally the same, one octave apart).

Discrete pitches, rather than continuously variable pitches, are virtually universal, with exceptions including "tumbling strains" (Sachs & Kunst, 1962) and "indeterminate-pitch chants" (Malm, 1967). Gliding pitches are used in most cultures, but are related to the discrete pitches they reference or embellish. (Burns, 1999)

Historical pitch standards

Historically, various standards have been used to fix the pitch of notes at certain frequencies. Various systems of musical tuning have also been used to determine the relative frequency of notes in a scale. In 1955, the International Organization for Standardization fixed the frequency of the A above middle C at 440 Hz, but in the past, various frequencies have been used.

Until the 19th century, there was no concerted effort to standardize musical pitch and the levels across Europe varied widely. Even within one church, the pitch used could vary over time because of the way organs were tuned. Generally, the end of an organ pipe would be hammered inwards to a cone, or flared outwards to raise or lower the pitch. When the pipe ends became frayed by this constant process, they were all trimmed down, thus raising the overall pitch of the organ.

Some idea of the variance in pitches can be gained by examining old tuning forks, organ pipes and other sources. For example, an English pitchpipe from 1720 plays the A above middle C at 380 Hz, while the organs played by Johann Sebastian Bach in Hamburg, Leipzig and Weimar were pitched at A = 480 Hz, a difference of around four semitones. In other words, the A produced by the 1720 pitchpipe would have been at the same frequency as the F on one of Bach's organs.

Pitch levels did not just vary from place to place, or over time - pitch levels could vary even within the same city. The pitch used for an English cathedral organ in the 17th century for example, could be as much as five semitones lower than that used for a domestic keyboard instrument in the same city.

Need to standardize pitch

The need to standardize pitch levels, at least within one city or country, rose as performance of music which combined the organ with instrumental ensembles became more popular. One way in which pitch could be controlled was with the use of tuning forks, although even here there was variation - a tuning fork associated with Handel, dating from 1740, is pitched at A = 422.5 Hz, while a later one from 1780 is pitched at A = 409 Hz, almost a semitone lower. Nonetheless, there was a tendency towards the end of the 18th century for the frequency of the A above middle C to be in the range of 400 to 450 Hz.

Throughout the first half of the 19th century, there was a tendency for the pitch used by orchestras to rise. This was probably largely due to orchestras competing with each other, each attempting to fill increasingly large concert halls with a brighter, more "brilliant", sound than that of their rivals. They were helped in this endeavour by the improved durability of the violins' E-strings - in the 16th century, Michael Praetorius had rejected various high pitch standards as leading to snapped strings, but the new strings could take the higher tension without breaking.

The rise in pitch at this time can be seen reflected in tuning forks. An 1815 tuning fork from the Dresden opera house gives A = 423.2 Hz, while one of eleven years later from the same opera house gives A = 435 Hz. At La Scala in Milan, the A above middle C rose as high as 451 Hz.

The most vocal opponents of the upward tendency in pitch were singers, who complained that it was putting a strain on their voices. Largely due to their protests, the French government passed a law on February 16, 1859 which set the A above middle C at 435 Hz. This was the first attempt to standardize pitch on such a scale, and was known as the diapason normal. It became quite a popular pitch standard outside of France as well.

There were still variations, however. The diapason normal resulted in middle C being tuned at approximately 258.65 Hz. An alternative pitch standard known as philosophical or scientific pitch, which fixed middle C at exactly 256 Hz (that is, 28 Hz), and resulted in the A above it being tuned to approximately 430.54 Hz, gained some popularity due to its mathematical convenience (the frequencies of all the Cs being a power of two). This never received the same official recognition as A = 435, however, and was not as widely used.

In 1939, an international conference recommended that the A above middle C be tuned to 440 Hz. This standard was taken up by the International Organization for Standardization in 1955 (and was reaffirmed by them in 1975) as ISO 16. The difference between this and the diapason normal is due to confusion over which temperature the French standard should be measured at. The initial standard was A = 439 Hz, but this was superseded by A = 440 Hz after complaints that 439 Hz was difficult to reproduce in a laboratory owing to 439 being a prime number.

Despite such confusion, A = 440 Hz is arguably the most common tuning used around the world. Orchestras in the United States and United Kingdom tend to adhere to this standard as concert pitch. In other countries, however, higher pitches have become the norm: A = 442 Hz is common in continental European orchestras, while A = 445 is heard in Germany, Austria, and China.

In practice, as orchestras still tune to a note given out by the oboe, rather than to an electronic tuning device (which would be more reliable), and as the oboist may not have used such a device to tune in the first place, there is still some variance in the exact pitch used. Solo instruments such as the piano (which an orchestra may tune to if they are playing together) are also not universally tuned to A = 440 Hz. Overall, it is thought that the general trend since the middle of the 20th century has been for standard pitch to rise, though it has certainly been rising far more slowly than it has in the past...

Readers should also consult Helmholtz: 'On the sensations of tone'.

Changing the pitch of a vibrating string

There are three ways to change the pitch of a vibrating string. String instruments are tuned by varying the strings' tension because adjusting length or mass per unit length is impractical.

Length

Pitch can be adjusted by varying the length of the string. A longer string will result in a lower pitch, while a shorter string will result in a higher pitch. The change in frequency is inversely proportional to the change in length, and a geometric change in length coresponds to an arithmetic change in frequency:

A string twice as long will produce a tone an octave lower.

Tension

Pitch can be adjusted by varying the tension of the string. A string with less tension (looser) will result in a lower pitch, while a string with greater tension (tighter) will result in a higher pitch. The change in frequency is proportional to the square root of the change in tension:

Density

The pitch of a string can also be varied by changing the density of the string. The change in frequency is inversely proportional to the square root of the change in density:

Sources

• Burns, Edward M. (1999). "Intervals, Scales, and Tuning", The Psychology of Music second edition. Deutsch, Diana, ed. San Diego: Academic Press. ISBN 0122135644.
• Sachs, C. and Kunst, J. (1962). In The wellsprings of music, ed. Kunst, J. The Hague: Marinus Nijhoff.
• Malm, W.P. (1967). Music Cultures of the Pacific, the Near East, and Asia. Englewood Cliffs, NJ: Prentice-Hall.
• Helmholtz, Hermann. (2005). On the Sensations of Tone as a Physiological Basis for the Theory of Music, Kessinger Publishing. ISBN 1419178938

External links

• String Tension and Tuning by Ian Noyce
• Tonalsoft Encyclopaedia of Tuning
• AthenaUtility Pitch Converter (AUpc) An athenaCL netTool for on-line, web-based pitch conversion from a variety of formats.
• String Tension on the Liutaio Mottola Lutherie Information Website