3.145.155.224
User Stats:
Today: 0
Yesterday: 0
This Month: 0
This Year: 0
Total Users: 117
New Members:
3.145.xxx.xxx
Server Time:
If a player bets on a single number and wins, the payout is 35 to 1. The bet itself is returned, so in total it is multiplied by 36. (In a lottery one would say 'the prize is 36 times the cost of the ticket', because in a lottery the cost of the ticket is not returned additionally.)
A player can bet on numbers, combinations, ranges, odds/evens, and colors.
Contents |
History of Roulette
Early roulette table, ca. 1800
The first form of roulette was first devised in 17th century France, by the mathematician Blaise Pascal, who was supposedly inspired by his fascination with perpetual motion devices. In 1842, fellow Frenchmen François and Louis Blanc added the "0" to the roulette wheel in order to increase house odds. Roulette was brought into the U.S. in the early 1800s, and again in order to increase house odds a second zero, "00", was introduced - although in some forms of early American roulette the double-zero was replaced by an American Eagle. In the 1800s, roulette spread all over both Europe and the U.S., becoming one of the most famous and most popular casino games. Some call roulette the "King of Casino Games", probably because it was associated with the glamour of the casinos in Monte Carlo. (François Blanc actually established the first casinos there).
A legend tells about François Blanc, who supposedly bargained with the devil to obtain the secrets of roulette. The legend is based on the fact that if you add up all the numbers on the roulette wheel (from 1 to 36), the resulting total is "666", which is the "Number of the Beast" and represents the devil.
Types of Roulette
There are two types of roulette, American roulette and European roulette. The difference between the two types is the number of 0's on the wheel. American roulette wheels have two "0's", zero and double-zero, which increases the house advantage to 5.3%. In European roulette there is only one zero, giving the house an advantage of 2.7%.
The two versions also use chips differently. American roulette uses so-called "non-value" chips, meaning that all chips belonging to the same player are of the same value determined at the time of the purchase, and the player cashes in the chips at the roulette table. European roulette uses standard casino chips of differing values as bets, which can make the game more confusing for both the croupier and the players.
A traditional European roulette table is also much larger than an American roulette table, and the croupier uses a long tool called a rake to clear out the chips and to distribute winnings. In American roulette the croupier collects and distributes chips by hand.
There is actually a third type of roulette wheel in use. It is a hybrid of the two versions described above, and is the only kind of wheel that is legal in the United Kingdom. This wheel has an American (English language) layout and a single zero. When a single-zero wheel is used in the United States, it is almost always this type.
Board depiction (American Roulette)
| 0 | ↔ | 00 | |||
| 1- 18 |
1st 12 |
1 | 2 | 3 | ← |
| 4 | 5 | 6 | ← | ||
| odd | 7 | 8 | 9 | ← | |
| 10 | 11 | 12 | ← | ||
| red | 2nd 12 |
13 | 14 | 15 | ← |
| 16 | 17 | 18 | ← | ||
| blk | 19 | 20 | 21 | ← | |
| 22 | 23 | 24 | ← | ||
| even | 3rd 12 |
25 | 26 | 27 | ← |
| 28 | 29 | 30 | ← | ||
| 19- 36 |
31 | 32 | 33 | ← | |
| 34 | 35 | 36 | ← | ||
| ↑ | ↑ | ↑ | |||
Bet odds table (American Roulette)
(in addition to the mentioned payout the bet is returned)
| Bet name | Winning spaces | Payout | Odds of winning (against) |
Expected value (on a $1 bet) |
|---|---|---|---|---|
| 0 | 0 | 35 to 1 | 37 to 1 | -$0.053 |
| 00 | 00 | 35 to 1 | 37 to 1 | -$0.053 |
| 1 | 1 | 35 to 1 | 37 to 1 | -$0.053 |
| 2 | 2 | 35 to 1 | 37 to 1 | -$0.053 |
| ... | ... | ... | ... | ... |
| 36 | 36 | 35 to 1 | 37 to 1 | -$0.053 |
| Row 00 | 0, 00 | 17 to 1 | 18 to 1 | -$0.053 |
| Row 3 | 1, 2, 3 | 11 to 1 | 11.667 to 1 | -$0.053 |
| Row 6 | 4, 5, 6 | 11 to 1 | 11.667 to 1 | -$0.053 |
| Row 9 | 7, 8, 9 | 11 to 1 | 11.667 to 1 | -$0.053 |
| ... | ... | ... | ... | ... |
| Row 36 | 34, 35, 36 | 11 to 1 | 11.667 to 1 | -$0.053 |
| Column 1 | 1, 4, 7, ..., 34 | 2 to 1 | 2.167 to 1 | -$0.053 |
| Column 2 | 2, 5, 8, ..., 35 | 2 to 1 | 2.167 to 1 | -$0.053 |
| Column 3 | 3, 6, 9, ..., 36 | 2 to 1 | 2.167 to 1 | -$0.053 |
| First 12 | 1, 2, 3, ..., 12 | 2 to 1 | 2.167 to 1 | -$0.053 |
| Middle 12 | 13, 14, 15, ..., 24 | 2 to 1 | 2.167 to 1 | -$0.053 |
| Last 12 | 25, 26, 27, ..., 36 | 2 to 1 | 2.167 to 1 | -$0.053 |
| Odd | 1, 3, 5, ..., 35 | 1 to 1 | 1.111 to 1 | -$0.053 |
| Even | 2, 4, 6, ..., 36 | 1 to 1 | 1.111 to 1 | -$0.053 |
| Red | 1, 3, 5, 7, 9, 12, 14, 16, 18, 19, 21, 23, 25, 27, 30, 32, 34, 36 |
1 to 1 | 1.111 to 1 | -$0.053 |
| Black | 2, 4, 6, 8, 10, 11, 13, 15, 17, 20, 22, 24, 26, 28, 29, 31, 33, 35 |
1 to 1 | 1.111 to 1 | -$0.053 |
| 1 to 18 | 1, 2, 3, ..., 18 | 1 to 1 | 1.111 to 1 | -$0.053 |
| 19 to 36 | 19, 20, 21, ..., 36 | 1 to 1 | 1.111 to 1 | -$0.053 |
| five number bet | 0, 00, 1, 2, 3 | 6 to 1 | 6.6 to 1 | -$0.079 |
Note also that 0 and 00 are neither odd nor even in this game.
House Edge
The house average or house edge is the amount the player loses relative to a bet, on average. If a player bets on a single number in the American game there is a probability of 1/38 that the player receives 36 times the bet (35 times the bet plus the return of the bet itself), so the player ends up, on average, losing 5.26% on each bet:
( (probability * payout) / bet ) - 1 = expected value as fraction of bet
For example, betting $10 on a single number on an American wheel:
( ((1/38) * 360) / 10 ) - 1 = -0.0526
The house has the same edge on all of the other kinds of bets, except for the five number bet where the house edge is considerably higher (7.89% on an American wheel).
The house edge should not be confused with the hold. The hold is the total amount that the house wins from a player. While the house might have an edge of 5.26%, if a player keeps playing until his or her bankroll is exhausted, the house will enjoy a hold of 100%.
Called Bets
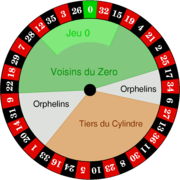Traditional roulette wheel sectors
There are a number of series in roulette that have special names attached to them. These are placed by betting a set amount per series (or multiples of that amount). They are based on the way in which certain numbers lie next to each other on the roulette wheel. Not all casinos offer these bets.
Voisins ("Neighbors")
This is a name for the numbers which lie between 22 and 25 on the wheel including 22 and 25 themselves. The series is 22,18,29,7,28,12,35,3,26,0,32,15,19,4,21,2,25 (on a single zero wheel).
9 chips or multiples thereof are bet.
Tiers ("The third")
This is the name for the numbers which lie on the opposite side of the wheel between 27 and 33 including 27 and 33 themselves. The series is 27,13,26,11,30,8,23,20,5,24,16,33 (on a single zero wheel).
6 chips or multipes thereof are bet.
Orphelins ("Orphans")
These numbers make up the two slices of the wheel outside the Tiers and Voisins. They contain a total of eight numbers, the Orphans comprising 17,34,6 and the Orphelins being 1,20,14,31,9.
8 chips or multiples thereof are bet.
Betting Strategies and Tactics
Albert Einstein is reputed to have stated, "You cannot beat a roulette table unless you steal money from it."
And yet, the numerous even money bets in roulette have inspired many players over the years to attempt to beat the game by using one or more variations of a Martingale betting strategy, wherein the gamer doubles the bet after every loss, so that the first win would recover all previous losses, plus win a profit equal to the original bet. As the referenced article on Martingales points out, this betting strategy is fundamentally flawed in practice and the inevitable long-term consequence is a large financial loss. There is no way such a betting strategy can work over the long term. Another strategy is the Fibonacci system, where bets are calculated according to the Fibonacci sequence. Regardless of the specific progression, no such strategy can ever overcome the casino's advantage; players trying them will inevitably lose sooner or later.
While not a strategy to win money, New York Times editor Andres Martinez described an enjoyable roulette betting method in his book on Las Vegas entitled "24/7". He called it the "dopey experiment". The idea is to divide your roulette session bankroll into 35 units. This unit is bet on a particular number for 35 consecutive spins. Thus, if the number hits in that time, you've won back your original bankroll and can play subsequent spins with house money. If your number never hits - well, it can take a great deal of time to spin the wheel 35 times; think of the fun you'll have in that time! In practice, this dopey experiment often results in funny looks from the dealer at first; soon, however, every gambler at the table will be putting money on your number. This turns roulette into a group activity that can rival craps for cheers when the number hits. However, there is only a (1 − (37 / 38)35) * 100% = 60.68% probability of winning within 35 spins (assuming a double zero wheel with 38 pockets).
There is a common misconception that the green numbers are "house numbers" and that by betting on them one "gains the house edge." In fact, it is true that the house's advantage comes from the existence of the green numbers (a game without them would be statistically fair) however they are no more or less likely to come up than any other number.
Various attempts have been made by engineers to overcome the house edge through predicting the mechanical performance of the wheel, most notably by Joseph Jagger, the man who broke the bank at Monte Carlo in 1873. These schemes work by determining that the ball is more likely to fall at certain numbers. Claude Shannon, a mathematician and computer scientist best known for his contributions to information theory, built arguably the first wearable computer to do so in 1961 [1].
To try to prevent exploits like this, the casinos monitor the performance of their wheels, and rebalance and realign them regularly to try to keep the result of the spins as random as possible.
More recently Thomas Bass, in his book The Newtonian Casino 1991, has claimed to be able to predict wheel performance in real time. He is also the author of The Eudaemonic Pie, which describes the exploits of a group of computer hackers, who called themselves the Eudaemons, who in the late 1970s used computers in their shoes to win at roulette by predicting where the ball would fall.
In the early 1990's, Gonzalo Garcia-Pelayo, realizing that most roulette wheels are not "perfect", used a computer to model the tendencies of the roulette wheels at the Casino de Madrid in Madrid, Spain. Betting the most likely numbers, along with members of his family, he was able to win over one million dollars over a period of several years. A court ruled in his favor when the legality of his strategy was challenged by the casino.
In 2004, it was reported that a group in London had used mobile cameraphones to predict the path of the ball, a cheating technique called sector targeting. [2] In December 2004 court adjudged that they didn't cheat because their special laser cameraphone and microchip weren't influencing the ball - they kept all £1.3m. [3]
Betting Only on Red
One conceivable strategy would be to bet on the ball landing in a red space for a certain number of spins, for example, 38.
There are 18 red spaces on a roulette table with 38 total spaces. Dividing 18 by 38 yields a probability of landing on red of 47.37%. This probability can be used in a binomial distribution and made into an approximate standard normal distribution.
Doing so indicates that, if one were to spin the wheel 38 times, there is a 99% probability that the ball would land on red at least 10 times. There is an 83% probability that in 38 spins, the ball will land on red at least 15 times. Out of 38 spins, there's a 50% chance that 18 will be red.
However, the break-even point is 19 spins, since the bet on red is 2:1, and the probability of 19 red spins in 38 is only 37%. This indicates the difficulty of winning by only betting on red.
The results occur because, as indicated by the 18 divided by 38 equals 47.37% figure, the ball will land on red less than half the time. This percentage applied in the binomial and standard normal distributions creates the vast divide in probability from 18 red spins to 19 red spins out of 38 spins. Basically, it is very unlikely for anyone to spin much more than 18 red spins out of 38 spins.
Betting multiple times
This type of bet is a combination of the red bet and the martingale system. Except this bet also includes the odd. What you do is you start off with a bet of 1 on each the red and the odd (or you can do the black and even). You treat each bet seperately. When one bet loses, you double it. When one bet wins, you set it back to 1. The reason that this technique keeps you in the game so long is that there is a 25% chance of you winning both the red and the odd and theres a 50% chance that you will break even. Of course in order for this method to last, you would need an unlimited source of money.
Famous Bets
- In 2004, Ashley Revell of London sold all of his possessions, clothing included, and brought US$135,300 to the Plaza Hotel in Las Vegas and put it all on "Red" at the roulette table in a double-or-nothing bet. The ball landed on "Red 7" and Revell walked away with his net-worth doubled to $270,600.
- In the 1942 film Casablanca, Rick's Café Americain has a trick roulette wheel. The croupier can cause it to land on 22 at will. Rick (Humphrey Bogart) urges a Bulgarian refugee with whose case he becomes sympathetic to put his last three chips on 22 and motions to the croupier to let him win. After the man's number dramatically comes up, Rick tells him to let it all ride on 22 and lets him win again. Although the details are not mentioned in the film (the croupier only notes that they are "a couple of thousand" down), it appears that Rick has given the man 3675 (3*35*35) francs.
- In the music video for Palace & Main by Kent, guitarist Harri Mänty goes to Las Vegas and bets the entire video budget on black. He wins, and the profits were donated to charity.
- In the third part of the 1998 film Run, Lola, Run, Lola uses all her money to buy a 100-mark chip. (She is actually just short of 100 marks, but gains the sympathy of a casino employee who gives her the chip for what money she has.) She bets her single chip on 20 and wins. She lets her winnings ride on 20 and wins again, making her total winnings 100,000 marks.
