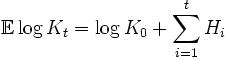Gambling Guide

Kelly gambling is an application of information theory to gambling and (with some ethical and legal reservations) investing. An important but simple relation exists between the amount of side information a gambler obtains and the expected exponential growth of his capital (Kelly). The so-called equation of ill-gotten gains can be expressed in logarithmic form as

for an optimal betting strategy, where K₀ is the initial capital, K_t is the capital after the tth bet, and H_i is the amount of side information obtained concerning the ith bet (in particular, the mutual information relative to the outcome of each betable event). This equation applies in the absence of any transaction costs or minimum bets. When these constraints apply (as they invariably do in real life), another important gambling concept comes into play: the gambler (or unscrupulous investor) must face a certain probability of ultimate ruin, which is known as the gambler's ruin scenario. Note that even food, clothing, and shelter can be considered fixed transaction costs and thus contribute to the gambler's probability of ultimate ruin.

This equation was the first application of Shannon's theory of information outside its prevailing paradigm of data communications (Pierce).